哇,你知道吗?在我们生活的三维世界里,竟然还隐藏着一个神秘的四维空间!今天,就让我带你一起探索这个奇妙的世界,揭开超正方体的神秘面纱。

什么是超正方体?
超正方体,又被称为Tesseract或Hypercube,是四维空间中的几何产物。简单来说,它就是立方体的四维版本。想象一个立方体有六个面,八个顶点和十二条边,那么超正方体就有十六个面、二十四条棱和三十二个顶点。是不是听起来就让人兴奋?
超正方体的存在
虽然我们无法直接感知四维空间,但数学家们已经证明了超正方体的存在。在数学的几何学中,有一个叫做拓扑空间的概念。在这个空间里,点是一维的,线是二维的,面是三维的,而体就是四维的。所以,超正方体就是由体组成的四维空间。

超正方体的投影
由于我们生活在三维空间,所以无法直接看到超正方体的真实面貌。但是,我们可以通过投影的方式来想象它。比如,我们可以将超正方体投影到三维空间中,这样就能看到它的三维投影了。
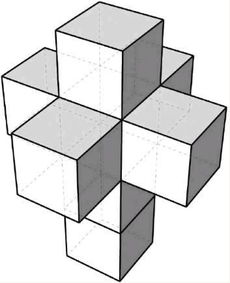
施莱格尔投影
施莱格尔投影是一种将四维图形投影到三维空间的方法。通过这种方法,我们可以看到超正方体的三维投影,它有八个胞体、二十四条棱和十六个顶点。虽然这个三维投影并不能完全展示超正方体的四维特性,但它已经足够让我们对超正方体有一个初步的认识了。
球极投影
球极投影是将超立方体的每个表面都膨胀一定的时间,从而得到一个超球。在这个超球中,我们可以看到超正方体的各个面。这种投影方式让我们仿佛置身于超正方体之中,可以更直观地感受到它的空间结构。
二维线架正投影
二维线架正投影是将超正方体投影到二维平面上。这种投影方式比较简单,只需要按照图上的相邻两个角都是45度,一个点一个点地画出来就可以了。
超正方体的展开图
如果你还是觉得超正方体很难想象,那么可以尝试画出它的展开图。就像我们研究三维图形的展开图一样,超正方体的展开图也是由八个立方体组成的。虽然看上去很困难,但只要耐心一点,你就能画出它来。
超正方体的意义
超正方体不仅仅是一个数学概念,它还与物理学、宇宙学等领域有着密切的联系。比如,在宇宙学中,超正方体被用来描述宇宙的结构。在物理学中,超正方体则被用来研究量子场论等问题。
超正方体是一个充满神秘色彩的几何产物,它让我们对四维空间有了更深入的了解。虽然我们无法直接感知四维空间,但通过数学和物理学的工具,我们仍然可以探索这个神秘的世界。让我们一起期待,未来有一天,我们能够真正走进四维空间,揭开它的神秘面纱!